压力和运动方程
压力和运动方程式简介
当固体变形时,内力会分布在材料中。这些被称为压力。压力具有每个区域的力单位。
在带有横截面的酒吧一种由轴向力加载F,力方向的压力是。作为日常观察,我们知道较厚的物体将能够维持更高的力量。因此,压力是一个直观的适当数量,用于提供有关材料的严重负载的信息。
除了上面所示,除了非常特殊的情况外,应力的大小和方向在整个载荷身体中都有不同。

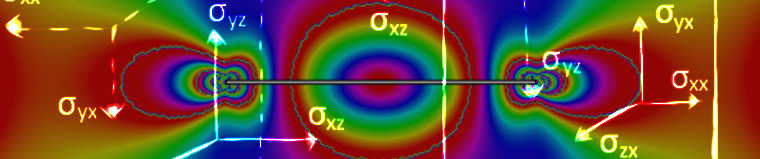
实验确定的应力模式围绕软材材料中的刚性包含。图片是使用光弹性获得的。SSMG-titery的图像。获得许可CC BY-SA 3.0, 通过Wikimedia Commons。
实验确定的应力模式围绕软材材料中的刚性包含。图片是使用光弹性获得的。SSMG-titery的图像。获得许可CC BY-SA 3.0, 通过Wikimedia Commons。
当力垂直于表面时,应力称为a正常应力。由作用于表面的力引起的压力称为剪切应力。
动量平衡
压力给出的身体内部力必须与外部力量和惯性力量一起按照牛顿的第二定律保持平衡。
让我们考虑一个在整个变形过程中由相同材料颗粒组成的小表面。我们假设变形而不会损失材料的连续性,因此不引入裂纹。变形之前,表面的特征是该区域da和正常矢量n。变形后,这些变成da和n。表面不一定是身体外部的一部分 - 它也可以是身体内部任何地方的概念表面。
作用在变形区域上的表面力可以表示为
这里,tn叫做牵引力, 尽管tn通常称为名义牵引力,因为它将作用在实际变形状态作用的力与未变形的区域相关联。
牵引力具有每个区域的单位力。如果该区域在变形过程中发生了变化,则两个牵引向量的幅度不同,但它们都具有相同的方向。
我们可以使用其空间组件编写名义牵引力t一世以及使用其材料成分的正常矢量nj。有关空间和物质框架的讨论,请阅读此信息关于变形分析的页面。
此外,我们将牵引成分写为正常向量的以下线性扩展:
在这里和下面的内容中,假定重复索引的求和。小型和资本指数分别用于空间和材料组件。
这样的表示有时被称为库奇定律或者库奇的公式。只有在pIJ是等级2的某些张量的组件。
对于任意未宣传的材料量v0,可以以以下整体形式表示动量保护:
在哪里代表重力或离心力等体积力,速度场是从位移场计算的,
, 作为
。
通过使用Cauchy的公式并应用发散定理,可以将表面积分转换为卷积分为:
由于卷是任意的,因此给出了动量平衡方程的以下差异形式:
或者,使用张量表示法:
张量p称为第一个Piola-Kirchhoff应力张量。它将作用在空间方向的力与原始未构型配置中的区域联系起来。因此,其组件由指代不同配置的索引给出。有时,这样的数学对象被称为两点张量。通常,该张量不是对称的。
类似的方法可以应用于牵引向量tn以及实际变形配置中的材料体积。这将导致以下表示:
张量称为Cauchy应力张量或者真正的应力张量,因为它代表了与实际变形区域相关的实际配置中的力。该张量由其空间成分表示。
如果我们考虑一个与空间坐标轴平行的较小区域,则Cauchy应力张量的成分的含义变得清晰。例如,第三个。然后,对该区域的正常向量为{0,0,1},牵引力由
因此,具有33个指数的应力张量分量使牵引向量分量在平面上的3个方向上具有正常的方向。具有两个相等指标的应力张量分量称为A正常应力或者直接应力。其他两个应力张量分量提供了对平面切线的牵引力的一部分。这样的组件称为剪切应力。
通过对小立方体进行瞬间平衡,可以证明cauchy应力张量是对称的,因此。只要没有体积力矩贡献,这是正确的。这样的材料被考虑使用科塞拉特理论, 存在。但是,它们并不常见。
由于考奇(Cauchy)和第一个piola-kirchhoff应力张量对应于同一表面力的不同表示,
为了找到两种压力措施之间的关系,我们可以使用南森的公式对于由于变形而导致的区域变化。它指出
在哪里F是个变形梯度张量和
体积因子j提供由变形引起的音量变化。因此,应力张量通过
可以通过引入称为The The的张量来进一步简化此和类似的公式Kirchhoff应力张量,定义为。Kirchhoff应力张量几乎没有实际用途,但更是理论上方便的数量。
质量保护和欧拉公式
就考克(Cauchy)压力张量而言,动量平衡方程可以写成
请注意,该方程式中的密度代表变形材料的真实密度。另外,体积力是每个变形体积的力。密度隐含地取决于由于群众保护作为
从计算的角度来看,这种增加的非线性使这种动量平衡方程的这种形式降低了有趣。
通过使用速度并将自变量更改为空间坐标X=X((X,t),我们到达
这是Eulerian配方中的动量平衡。这样的公式通常在流体动力学,其中速度被视为因变量。
机械能量平衡
将动量方程的差异形式乘以速度向量并将其整合到材料上,给出以下方程:
这个方程式显示了不可或缺的形式机械能量平衡。也称为驱动定理。速度的空间梯度是和:操作员指示两个指数的总结;
。详细讨论了速度梯度的属性变形页面分析。
方程右侧的两个积分分别表示体积和表面力的功率输入。这种功率输入是各自力量对材料上完成的每单位时间的工作。
左侧的术语分别是动能变化的速率和所提供的应力功率。对于弹性材料,应力功率是应变能密度的变化速率。
通过使用关系
应力能力可以以以下等效形式表示:
因此,我们可以说第一个piola-kirchhoff应力张量和变形梯度形成能量共轭对。这样的对也可以称为功率共轭或者工作共轭压力和应变度量。
速度梯度可以分解为对称和反对称部件,称为应变率张量((ld) 和自旋张量((lw), 分别。由于Cauchy应力张量是对称的,因此。因此,与库奇应力偶联的应变度量是应变率张量。后者也可以写为
在哪里
是个绿色 - 拉格朗日应变张量。然后,压力能力积分可以被重写为:
这里
称为第二Piola-Kirchhoff应力张量。这是一种对称张量,与绿色 - 拉格朗日菌株的能量共轭。
第一和第二Piola-kirchhoff应力张量通过:
此公式使得可以重写动量平衡方程为:
与形式的构成关系
将为位移向量提供一个封闭的方程式系统。
旋转平面上的应力成分
对于轴加的杆,很容易考虑压力作为标量数,并指出在此条上,只有正常的应力。全部压力张量是
该应力张量具有与坐标系中表达的组件X- 轴与条对齐。在任何其他坐标系中,都会有正常应力和剪切应力的混合物。如果我们考虑不垂直于杆轴的概念内表面,这可以看见。在该表面上,实际上将同时存在正常(σ)和剪切(τ)应力,如下图所示。
在旋转的系统中,其第一轴与正常与表面对齐,应力张量具有结构
在哪里是条形轴和正常表面之间的角度。
这样的压力状态通常被称为单轴。但是,只有在某个坐标系中才能由单个正常应力分量表示。
比较库奇和第二piola-kirchhoff应力
让我们考虑一种正交材料。该材料沿着直悬臂梁的特定取向含有纤维。
由于它是沿着材料方向定义的,因此即使结构发生旋转,第二Piola-Kirchhoff应力也将使我们能够在纤维方向上可视化应力。
在下图中,梁是通过尖端施加的纯矩弯曲的。我们可以看到Cauchy应力和第二Piola-Kirchhoff应力的11个组成部分。弯曲应力沿着梁物理定向,因此,随着偏转的发生,与空间固定的水平方向相关的Cauchy应力的11组分降低。另一方面,第二个piola-kirchhoff应力在整个光束上具有相同的厚度分布,也具有变形的构型。
第二Piola-Kirchhoff应力的实际值更难解释,因为它与原始区域或变形区域无关。
发布:2018年4月19日最后修改:2018年4月19日
